Glass Half Empty:

Glass Half Empty

What if a glass of water was, all of a sudden, literally half empty?
—Vittorio Iacovella

The pessimist is probably more right about how it turns out than the optimist.

When people say “glass half empty”, they usually mean something like a glass containing equal parts water and air:



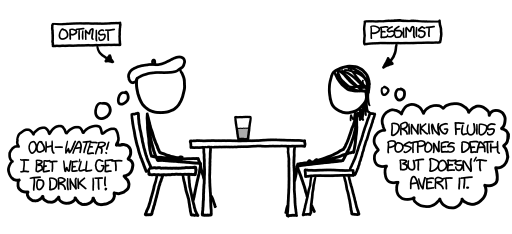
Traditionally, the optimist sees the glass as half full while the pessimist sees it as half empty. This has spawned a zillion joke variants—e.g., the engineer sees a glass that’s twice as big as it needs to be, the surrealist sees a giraffe eating a necktie, etc.

But what if the empty half of the glass were actually empty—a vacuum? (Even a vacuum arguably isn’t truly empty, but that’s a question for quantum semantics.)

The vacuum would definitely not last long. But exactly what happens depends on a key question that nobody usually bothers to ask: Which half is empty?

For our scenario, we’ll imagine three different half-empty glasses, and follow what happens to them microsecond by microsecond.



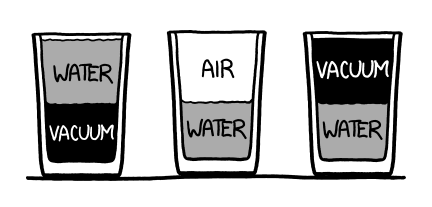
In the middle is the traditional air/water glass. On the right is a glass like the traditional one, except the air is replaced by a vacuum. The glass on the left is half full of water and half empty—but it’s the bottom half that’s empty.

We’ll imagine the vacuums appear at time t=0.



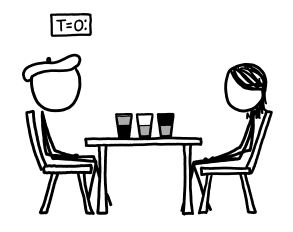
For the first handful of microseconds, nothing happens. On this timescale, even the air molecules are nearly stationary.



For the most part, air molecules jiggle around at speeds of a few hundred meters per second. But at any given time, some happen to be moving faster than others. The fastest few are moving at over 1000 meters per second. These are the first to drift into the vacuum in the glass on the right.

The vacuum on the left is surrounded by barriers, so air molecules can’t easily get in. The water, being a liquid, doesn’t expand to fill the vacuum in the same way air does. However, in the vacuum of the glasses, it does start to boil, slowly shedding water vapor into the empty space.



While the water on the surface in both glasses starts to boil away, in the glass on the right, the air rushing in stops it before it really gets going. The glass on the left continues to fill with a very faint mist of water vapor.



After a few hundred microseconds, the air rushing into the glass on the right fills the vacuum completely and rams into the surface of the water, sending a pressure wave through the liquid. The sides of the glass bulge slightly, but they contain the pressure and do not break. A shockwave reverberates through the water and back into the air, joining the turbulence already there.



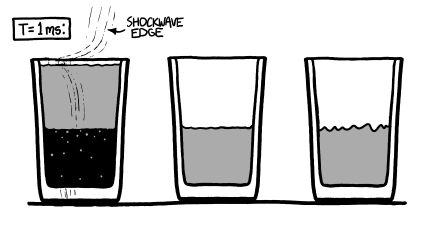
The shockwave from the vacuum collapse takes about a millisecond to spread out through the other two glasses. The glass and water both flex slightly as the wave passes through them. In a few more milliseconds, it reaches the humans’ ears as a loud bang.



Around this time, the glass on the left starts to visibly lift into the air.


The air pressure is trying to squeeze the glass and water together. This is the force we think of as suction. The vacuum on the right didn’t last long enough for the suction to lift the glass, but since air can’t get into the vacuum on the left, the glass and the water begin to slide toward each other.



The boiling water has filled the vacuum with a very small amount of water vapor. As the space gets smaller, the buildup of water vapor slowly increases the pressure on the water’s surface. Eventually, this will slow the boiling, just like higher air pressure would.



However, the glass and water are now moving too fast for the vapor buildup to matter. Less than ten milliseconds after the clock started, they’re flying toward each other at several meters per second. Without a cushion of air between them—only a few wisps of vapor—the water smacks into the bottom of the glass like a hammer.



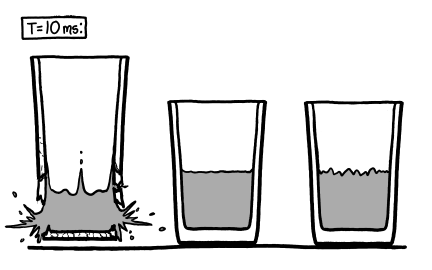
Water is very nearly incompressible, so the impact isn’t spread out—it comes as a single sharp shock. The momentary force on the glass is immense, and it breaks.

This “water hammer” effect (which is also responsible for the “clunk” you sometimes hear in old plumbing when you turn off the faucet) can be seen in the well-known party trick (recorded on Mythbusters, analyzed in physics classes, and demonstrated in countless student dorms) of smacking the top of a glass bottle to blow out the bottom.

When the bottle is struck, it’s pushed suddenly downward. The liquid inside doesn’t respond to the suction (air pressure) right away—much like in our scenario—and a gap briefly opens up. It’s a small vacuum—a few fractions of an inch thick—but when it closes, the shock breaks the bottom of the bottle.

In our situation, the forces would be more than enough to destroy even the heaviest drinking glasses.



The bottom is carried downward by the water and thunks against the table. The water splashes around it, spraying droplets and glass shards in all directions.

Meanwhile, the detached upper portion of the glass continues to rise.



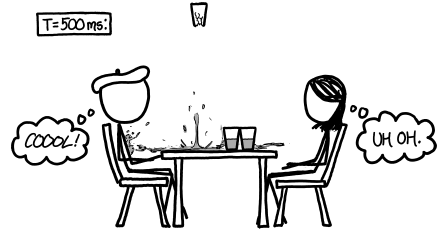
After half a second, the observers, hearing a pop, have begun to flinch. Their heads lift involuntarily to follow the rising movement of the glass.



The glass has just enough speed to bang against the ceiling, breaking into fragments…



… which, their momentum now spent, return to the table.



The lesson: If the optimist says the glass is half full, and the pessimist says the glass is half empty, the physicist ducks.